A construção de uma carteira ótima não é tarefa simples. Há décadas pesquisadores discutem maneiras de se ponderar os diversos ativos de forma a alcançar o que se chama de carteira eficiente. Ou seja, aquela que produz o maior retorno por unidade de risco.

O artigo de Harry Markowitz de 1952, intitulado “Portfolio Selection”, é conhecido como marco inicial do que hoje é conhecida como Teoria Moderna de Portfólio. Markowitz ganhou o prêmio Nobel em economia de 1990 por seu trabalho.

Conforme descrito por Markowitz, o processo de construção de portfólio se divide em duas etapas. A primeira é a estimação de três variáveis. A segunda é a combinação ótima destas de forma a obter o máximo retorno para o nível de risco selecionado. Discuto abaixo as três variáveis que você precisa estimar para ter esta carteira.

O procedimento pode ser utilizado para construção de portfólios de quaisquer ativos de risco, por exemplo apenas ações ou classes de ativos. Exemplos de classe de ativos são: renda fixa prefixado, renda fixa referenciada à inflação, crédito internacional, ações nacionais, ações globais, fundos imobiliários, commodities e outros.

O objetivo é construir a fronteira eficiente representada pela linha azul na figura abaixo. Para construir este conjunto de combinações ótimas, foram utilizados os ativos marcados pelos pontos em asterisco da cor amarela. Neste exemplo, os ativos em amarelo são classes de ativos diferentes.

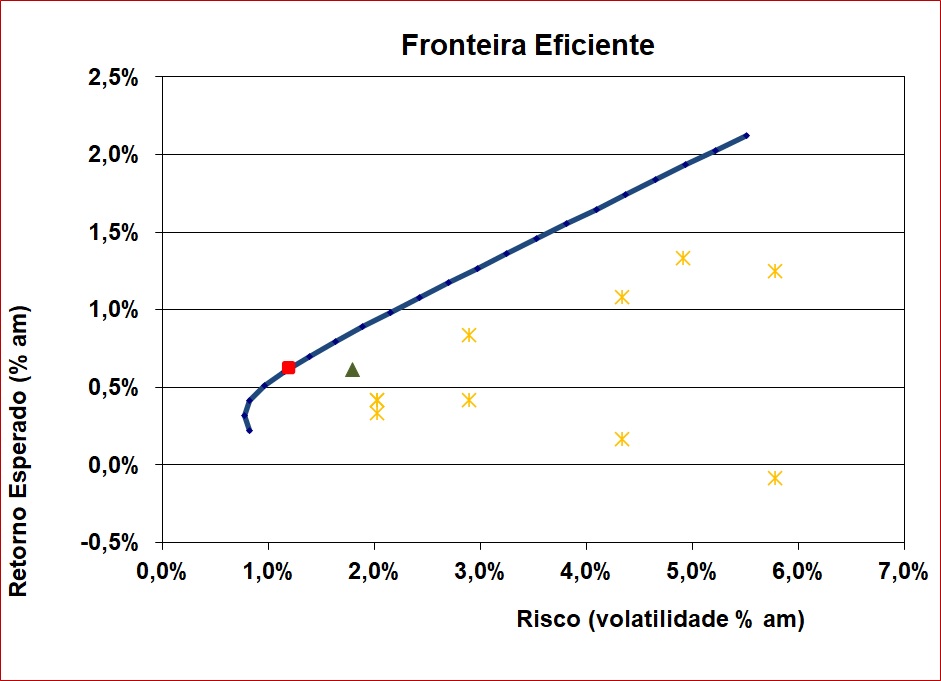
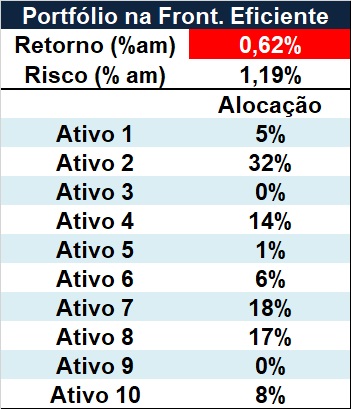
Cada ponto em cima da fronteira (linha azul) indica o maior retorno esperado que é possível ser alcançado dado o risco escolhido. Por exemplo, o ponto vermelho representa o portfólio descrito na tabela abaixo.

Perceba no gráfico que os ativos em amarelo isoladamente são escolhas piores em termos de retorno, considerando seu risco. Ou seja, um investidor nunca deveria investir em um destes ativos individualmente, pois há uma combinação que produz mais retorno com mesmo risco, que está em cima da fronteira eficiente.

Para entender o poder da combinação ótima veja o ponto indicado por um triangulo verde no gráfico acima. Ele possui o mesmo retorno esperado que o ponto vermelho na fronteira, mas possui maior risco. Este ponto foi obtido a partir de uma ponderação igual nos dez ativos, ou seja, 10% em cada um.

Para se construir a fronteira, é necessário estimar três variáveis: retorno esperado, risco – medido pelo desvio padrão – e correlação entre os ativos.

Quando se faz uma estimativa de retorno para um ativo, não é possível ter certeza sobre este retorno. Portanto, o que se faz é criar uma distribuição de probabilidades de retorno como a apresentada na figura abaixo. O retorno médio é o ponto no meio desta distribuição. A dispersão dos retornos em relação a esta média é a medida de risco.

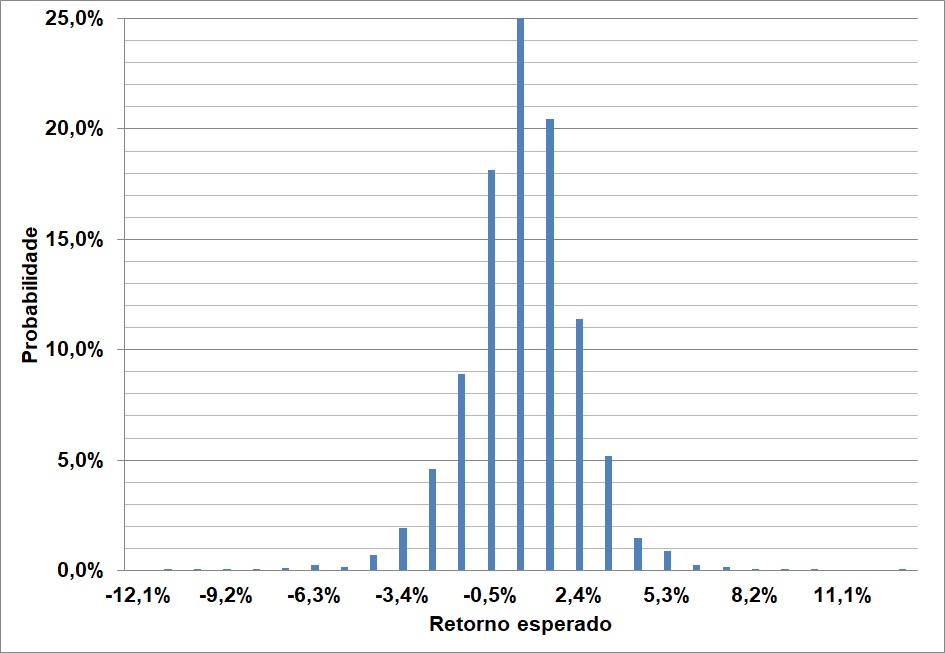
Para a construção da fronteira acima, utilizou-se as seguintes medidas de retorno e risco.

Perceba que o ativo 2 possui um retorno muito baixo e mesmo risco do ativo 1. No entanto, na alocação indicada na fronteira, foi atribuído um peso muito superior a ele. Parece intrigante, concorda?

A razão para isso reside na terceira variável que é a correlação entre os retornos. A correlação é a medida de relação linear entre os retornos dos ativos. Ela varia entre -1 e 1.

Uma correlação perfeita de 1 entre dois ativos significa que sempre que o retorno de um ativo é positivo, o do outro também é. Assim como sempre que o retorno de um for negativo, o do outro também será.

A matriz de correlação entre os ativos utilizado para construção desta fronteira está apresentada abaixo.

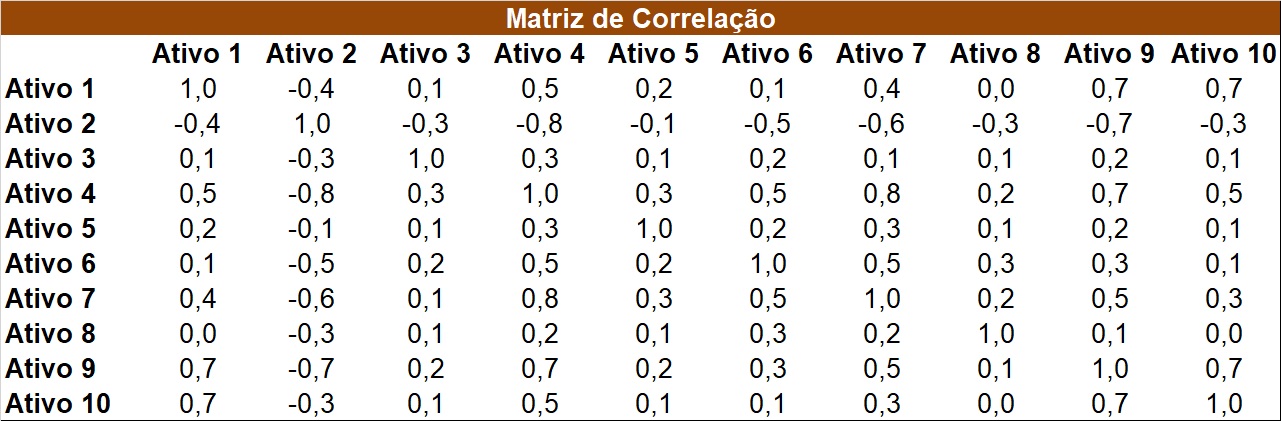
Perceba que a correlação do ativo 2 com os outros é negativa. Portanto, ele se comporta como um ativo de “proteção” e, por isso, foi alocado maior peso a ele.

Estimar as variáveis estatísticas dos ativos e ponderá-los de forma a obter a melhor alocação é o trabalho de gestores e alocadores de recursos.

Michael Viriato é professor de finanças do Insper e sócio fundador da Casa do Investidor.